Intro - "Laser-Diane" baut einen Fusor?

Ich gebe zu, daß ich ein bißchen faul bin.
Und ich gebe auch zu, daß ich mal über den Argon-Ionenlaser gesagt habe, daß er mit seiner Plasma-Temperatur von 30.000 Grad in der Kapillare die Grenze dessen sei, was Amateure bauen können. "Der nächste Schritt wäre dann der Fusionsreaktor", sagte ich damals im Spaß. Nun, wenn ich geahnt hätte...
Nach 15 Jahren Laserbastelei und einer ganzen Reihe von funktionierenden Lasern war der nächste Laser nicht mehr so die große Herausforderung für mich. Ok, es gibt noch einige, die ich gern bauen würde, aber mal ein anderes Projekt wäre auch nicht schlecht, dachte ich. Ohne dabei gleich mit einer kompletten Neuaustattung meines Labors zu beginnen zu müssen, versteht sich natürlich. Und dann stolperte ich unversehens über eine Kopie der berühmten Anleitung von R. Hull über den Selbstbau eines Farnsworth-Hirsch-Fusors.
Ein Amateur-Fusionsreaktor? - ("Ähem... jaa, Schatz...")
Genau das habe ich auch zuerst gedacht, liebe Leserin, aber zunächst einmal weitergelesen. Die Stirn gerunzelt. Und recherchiert. Und begriffen, daß es wirklich geht. Ein lohnendes nächstes Projekt.
Allerdings...
Die Anleitungen zum Selbstbau eines Fusors, die im Web verfügbar sind, hatten für mich ein paar kleine Schönheitsfehler.

Ich wollte nicht meine liebgewonnene einstufige Vakuumpumpe, immerhin vom ersten regulären Gehalt meines Lebens bezahlt, gegen eine neue zweistufige austauschen.
Meine selbstgemachte Hochspannungsversorgung wollte ich auch nicht neubauen.
Eigentlich interessiert mich die Produktion von Neutronen nicht nur überhaupt nicht, ich halte sie auch für unnötig gefährlich für eine Amateurin. Abgesehen davon hab ich kein einziges geeignetes Strahlungsmeßgerät. Und ein Faß für radioaktiven Abfall (vulgo "Atommüll") paßt auch nicht in meinen Keller.
Schließlich störte mich etwas der Alibi-Begriff "Demo-Fusor". Ein Fusor, der nicht fusioniert, ist keiner, sondern ein Ionen-Multipaktor oder eine sphärische Fokusdiode. Sie dürfen hier gerne über die Pingeligkeit der Mathematikerin lächeln, liebe Leserin. Bedenken Sie jedoch: ein Laser, der keinen Laserstrahl erzeugt, heißt auch nicht "Demo-Laser". Sondern Leuchtdiode, Neonröhre oder Schrott.

Also, mein Fusor, falls es einer werden sollte, müßte sich seinen Namen schon verdienen.
Aber darüber hinaus ist ein Fusor ein sehr hübsches Ding. Ein kleiner künstlicher Stern in einer Retorte, Transmutation der Elemente, außerordentlich romantisch. Was die obigen Schönheitsfehler betrifft, das muß doch auch anders gehen?! Natürlich behaupten alle, daß es nicht anders geht, aber hatten nicht auch 1982 alle zu mir gesagt, daß eine Amateurin keinen Laser selbstbauen kann?
Ein wenig weitere Recherche in alten Physikbüchern und astrophysikalischen Zeitschriften brachte mich auf die Spur von Helium. Eine Entladung in Helium hat den Vorteil, auch bei höherem Druck schon die spannenderen Niederdruck-Phänomene zu zeigen, da es von allen Gasen geladenen Partikeln die größten freien Weglängen gestattet. Darüber hinaus ist es in Form von Ballon-Helium unschlagbar billig.
Ja, und gab es da nicht eine Kernreaktion, bei der sich aus drei Heliumkernen Kohlenstoff bildet, und zwar ohne lästige Neutronen auszuwerfen...?
Und hatte ich nicht eine Menge Erfahrung damit gesammelt, Lasern mit Hilfe sehr kurzer und sehr starker Pulse auf die Sprünge zu helfen - das sollte bei einem Fusor doch auch gehen...?
Kurz gesagt, ich hatte eine Menge neuer Ideen, wie das immer ist, wenn zwei verwandte Disziplinen aufeinandertreffen. Was dabei herausgekommen ist, was geklappt und nicht geklappt hat, das schreibe ich hier nieder.
Daß Kohlenstoff nicht dabei herauskommt, jedenfalls nicht während meiner verbleibenden Lebenszeit, zeigte sich recht schnell schon anhand einiger Berechnungen (s.u.), aber es gibt immerhin die Chance auf den ersten Teilschritt der Reaktion, bei der sich temporär Beryllium-8 bildet. Nur etwa ein Atom alle paar Minuten, und es zerfällt auch praktisch sofort wieder in zwei Heliumkerne. Aber das genügt mir, damit mein Fusor sich seinen Namen verdient.
Und ich bin mir ziemlich sicher, daß es andere Methoden gibt, die aberwitzigen Temperaturen im Plasmafokus nachzuweisen als ausgerechnet Neutronenstrahlung von Deuteriumfusion. Auch wenn es, so wie's aussieht, nicht möglich ist, die Bildung von Beryllium-8 direkt nachzuweisen.

Teil I: Theorie und vorbereitende Experimente

Fusor-Grundlagen

Im Internet lassen sich viele Informationen über die Funktionsweise eines Fusors finden, beispielsweise über Wikipedia oder fusor.net, ich gebe deshalb hier nur eine knappe Übersicht.

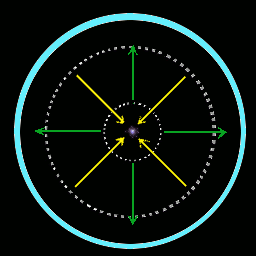Diagramm 1.
Schematischer Aufbau eines Fusors im Querschnitt. Das Vakuumgefäß ist hellblau markiert, die gepunkteten Linien bezeichnen die Elektrodengitter. Die Wege der Elektronen bzw. positiven Ionen sind durch grüne und gelbe Pfeile dargestellt. In der Mitte bezeichnet das grauviolette Wölkchen die Position des Plasmafokus (auch Poissor genannt).

Ein Fusor ist im Prinzip nichts weiter als eine Neonleuchtreklame in sehr ungewöhnlicher Form, nämlich mit zwei kugelförmig ineinanderliegenden Elektroden. Solche sphärischen Fokusdioden wurden schon in den 1920er Jahren von Katherine Blodgett und Irvine Langmuir untersucht, und schon damals wurde die Bildung eines leuchtenden Punktes in der Mitte der Kugeln bemerkt, aber noch nicht weiter untersucht. Das tat erst in den 1950er Jahren Philo Farnsworth, der darin eine Möglichkeit sah, zu einem funktionierenden Fusionsreaktor zu gelangen (er benutzte übrigens auch als erster die Bezeichnung "Fusor"). Farnsworth und seine Mitarbeiter konnten die Kernfusion mit ihren Versuchsaufbauten demonstrieren, schafften es jedoch nicht, auch nur in die Nähe einer Netto-Energieerzeugung zu gelangen. Die Förderung für die Forschung wurde Ende der 1960er Jahre eingestellt.
Erst in den 1990er Jahren wurde der Fusor "wiederentdeckt" und seitdem u.a. als kommerzielle Neutronenquelle hergestellt. Wegen seines einfachen Aufbaues hat er seitdem auch eine "Fangemeinde" von Amateurexperimentatoren.

Die Funktion eines Fusors ist nicht schwer zu verstehen. Im Prinzip besteht er nur aus einer meist kugelförmigen Vakuumkammer mit zwei ineinanderliegenden grobmaschigen kugelförmigen Gittern als Elektroden darin. Wird an die Gitter eine Hochspannung von einigen tausend Volt angelegt, meist ist dabei das kleinere innere Gitter der Minuspol, dann zündet bei genügend niedrigem Gasdruck in der Kammer ebenso wie in einer gewöhnlichen Neonröhre eine Glimmentladung zwischen den Elektroden. Dabei wandern Elektronen in Richtung des positiven äußeren Gitters (grün im obigen Diagramm). Bei Zusammenstößen mit den Gasatomen entstehen dabei auch positiv geladene Ionen, die sich in Richtung des negativen inneren Gitters bewegen.
Wenn der Gasdruck in der Kammer sehr niedrig ist, gibt es nur noch wenige Zusammenstöße von Ionen und Elektronen mit neutralen Atomen des Gases (die mittlere freie Weglänge wird ziemlich groß). Es kann dann passieren, daß die Teilchen den gesamten Weg zwischen den Gittern in gerader Linie fliegen und dabei sehr schnell werden. Am Gitter angekommen, werden die meisten durch eine Masche schlüpfen und in derselben Richtung weiterfliegen.
Im Fall der Elektronen führt das dazu, daß sie auf die Wand der Kammer prallen. Bei dieser abrupten Bremsung entsteht Wärme und Röntgenstrahlung, und im Falle einer Wand aus Glas auch eine bläuliche Fluoreszenz. Da in der Praxis der Aufbau nie exakt kugelförmig ist und zudem Elektronen sich durch äußere Störungen (wie Magnetfelder) leicht ablenken lassen, neigen sie dazu, sich an bestimmten Stellen zu bündeln. Die Wand einer Plastikkammer wird dabei sehr leicht durchgebrannt, ein Grund, warum billige Exsikkatoren aus Plastik nur sehr eingeschränkt als Kammer für einen Fusor taugen.
Eine Glaswand läßt ab einer bestimmten Energie die Röntgenstrahlung entweichen, deswegen sollte in solchen Fällen die Hochspannung begrenzt werden oder eine Bleiabschirmung eingeplant werden.

Anders als die Elektronen, die sich über die gesamte Außenwand verteilen (zumindest theoretisch), sammeln sich die durchgeschlüpften positiven Ionen alle im Mittelpunkt der Kugel, wo sie aus allen Richtungen kommend mit hoher Geschwindigkeit zusammenprallen. Dann bildet sich ein sehr heißer Plasmafokus, der als leuchtender Punkt sichtbar wird. Ein solcher Versuchsaufbau heißt, wie oben schon erwähnt wurde, sphärische Fokusdiode.
Wenn der Gasdruck noch weiter erniedrigt wird, verlängert sich die freie Weglänge der Ionen noch weiter. Egal, ob im Zentrum ein Ion von einem anderen abgeprallt ist oder es einfach nur durchgeflogen ist, egal, welche Richtung es aus der Mitte wegfliegt, in dem Moment, wenn es wieder durch eine Masche im inneren Elektrodengitter schlüpft, wird es von der positiven äußeren Elektrode abgestoßen und somit gebremst. Das passiert solange, bis es zum Stillstand gekommen ist und sich seine Bewegungsrichtung umkehrt. Das Ion fliegt nun wieder in Richtung Mitte, bereit für eine neue Chance auf eine Kollision. Einen solchen Aufbau nennt man Ionen-Multipaktor. Der Trick, durch die elektrische Abstoßung die Ionen gewissermaßen im Inneren der Kammer gefangenzuhalten, heißt elektrostatischer Trägheits-Einschluß oder englisch intertial electrostatic confinement, kurz IEC.
Wenn der Aufbau der Kammer sehr präzise ausgerichtet ist, kann in dem Plasmafokus eine ziemlich hohe Dichte von Ionen erreicht werden. Bei genügend hoher Geschwindigkeit der Ionen kann die Energie bei einem frontalen Zusammenstoß ausreichen, um sogar die elektrostatische Abstoßung zwischen den Atomkernen so weit zu überwinden, daß die Kerne verschmelzen können. In diesem Augenblick, in dem im Plasmafokus die Chance einzelner Kernfusionen besteht, kann man bei dem Versuchsaufbau von einem Fusor sprechen.
Technisch ist dabei von Vorteil, daß Ionen, die "nicht getroffen" haben, durch das oben erklärte Einschluß-Prinzip des Multipaktors eine neue Chance bekommen. Leider liegt genau darin auch das Hauptproblem des Fusors: für jeden neuen Versuch müssen die Ionen am inneren Gitter vorbei. Und so weit die Maschen darin auch sein mögen, irgendwann treffen sie dabei auch einen Draht. Die Energie des Ions geht dann verloren.
Üblicherweise werden die inneren Gitter von Fusoren dadurch weißglühend im Betrieb, was ein großes Problem für die Haltbarkeit darstellt. Ein Konzept aus neuerer Zeit von Robert Bussard sieht vor, die Gitter durch Magnetfelder zu schützen.
In letzter Zeit gibt es Anzeichen dafür, daß ein weiterer störender Effekt im Fusor stärker ist als anfänglich gedacht. Durch die Kollisionen der Ionen im Plasmafokus prallen die Partikel nämlich mit sehr unterschiedlichen Geschwindigkeiten zurück. Hatten im Idealfall am Anfang alle Ionen fast die gleiche Geschwindigkeit, so werden nach einer Reihe von Kollisionen die Geschwindigkeiten sehr unterschiedlich sein. Ähnlich wie in einer normalen Flamme werden zwar die meisten Teilchen eine mehr oder weniger durchschnittliche Geschwindigkeit haben, es wird aber auch ziemlich viele langsame oder sehr schnelle geben. Diesen Vorgang nennt man Thermalisierung, und offensichtlich passiert er sehr viel schneller als man das ursprünglich erwartet hatte.
Die schnelleren Partikel sind in diesem Fall genau das Problem, denn sie können genug Energie gesammelt haben, um der Abstoßung durch das äußere Gitter zu widerstehen und damit dem Einschluß zu entkommen. Auch ihre Energie geht dann dem Kreislauf verloren.
Bisher haben alle diese Probleme dafür gesorgt, daß der Fusor noch nicht als Energiequelle nutzbar ist.

Glimm- und Kathodenstrahlröhre

Während der Zeit, in der ich Laser gebaut habe, hatte ich selten mit sehr niedrigen Drücken unter ca. 266 Pa (veraltet: 2 Torr) zu tun. Es bot sich daher an, zunächst ein paar Vorversuche mit einfachen Glimmentladungsröhren zu machen. Im Prinzip habe ich mit den Lasern in den 1980er Jahren so ähnlich angefangen: praktische Erfahrung mit einer Vakuumapparatur kann man nicht aus Büchern lernen.

Bild 1.
Experimentalaufbau für eine einfache Glimmentladung in Luft bei ca. 20 Pa (veraltet: 0,15 Torr oder 150 Micron). Im Bild sichtbar sind sind der Leuchtreklame-Transformator und der Spannungsverdoppler, einige Druckmeßgeräte und die Vakuumpumpe.

Bei Drucken unter 133 Pa (1 Torr) kann man dabei schon die klassische Struktur einer Glimmentladung erkennen (oben im eingesetzten Bild von links nach rechts:), die langezogene positive Säule, in Luft rosaviolett, die den Hauptteil der Entladung ausmacht, dann den Faradayschen Dunkelraum, der den Übergang zu dem blauvioletten negativen Glimmlicht darstellt. Zwischen letzterem und der Kathode befindet sich dann noch der Hittorfsche (auch: Crookesche oder Kathoden-) Dunkelraum.
Für Amateure ist es immer lohnend, die Literatur aus der Zeit zu durchforsten, in der eine bestimmte Forschungsdisziplin gerade erst entdeckt worden war - in dieser Zeit waren nämlich auch die professionellen Forscher noch Anfänger, und man kann ihren Arbeiten wertvolle Hinweise entnehmen. Das betrifft die Bedingungen, bei denen sich Kathoden- bzw. Elektronenstrahlen bilden oder auch Kanal- bzw. Ionenstrahlen. Bei Glimmentladungen stößt man schnell darauf, daß Helium für solche Untersuchungen sehr beliebt war, denn es hat die verblüffende Eigenschaft, durch Elektronenstrahlen zu grünem und durch Ionenstrahlen zu elfenbeingelbem Leuchten angeregt zu werden, während die positive Säule rosa ist. Die verschiedenen Phänomene lassen sich also leicht identifizieren.
Noch einen anderen Vorteil hat Helium. Man macht beim Experimentieren schnell die Erfahrung, daß in einer Glimmentladung die leuchtenden Zonen an der Kathode sich ausdehnen, wenn der Druck gesenkt wird. In Helium sind diese Zonen jedoch von Anfang an viel ausgedehnter als in anderen Gasen, man hat gewissermaßen einen "Druckbonus".
Die Ausdehnung der Zonen läßt sich sogar zur Druckmessung heranziehen. Es gibt nämlich die Beobachtung, daß in einer Glimmentladung für eine konstante Spannung das Produkt aus Druck und der Länge des Kathodendunkelraumes konstant ist:

p * d = const.

Untersuchungen aus den 1920er Jahren zeigen dabei, daß die Konstante bei hohen Spannungen (>2kV) kaum noch von der Spannung selbst abhängt, allerdings sehr wohl vom Gas. Man findet dann für die Konstante

Helium	533	Pa * mm
Wasserstoff	266	Pa * mm
Luft, Argon, ...	133	Pa * mm

Helium bringt also einen ziemlichen Bonus: eine Entladung in 13 Pa (veraltet 0.1 Torr oder 100 Micron) Helium zeigt also dieselbe Ausdehnung wie in 3.25 Pa (alt 0.025 Torr, 25 Micron) Luft. Bei einem Fusor können dazwischen schon Welten liegen...
Nebenbei bemerkt zeigt die Entladung damit im Prinzip auch von selbst an, bei welchem Druck sie stattfindet. Da sich an den kugelförmigen Fusorgittern die Länge des Kathoden-Dunkelraumes nur schlecht schätzen läßt, bietet sich an, eine Hilfskathode in einem Seitenarm des Gefäßes anzubringen, bei der sich d leicht messen läßt. Fertig ist ein einfaches Meßgerät für den Druckbereich von rund 266 bis 7 Pa.

Bild 2.
In diesem Bild wurde die einfache Glimmröhre durch eine gelochte Anode und einen Kolben dahinter erweitert. Eine Nachfüllkartusche für Partyballons dient als Heliumreservoir.
Man beachte die massiven Kühlkörper an der Anode.

Mit diesem Wissen bastelte ich mir für die nächsten Versuche eine einfache Kathodenstrahlröhre. Sie funktionierte, abgesehen von kleineren technischen Problemen durch die Erwärmung, überraschend gut. Mit einer Heliumfüllung von 40 Pa (0.3 Torr) bildet sich ein kräftiger Elektronenstrahl, der sich als grüne Fluoreszenz im Kolben und durch einen blauen Leuchtfleck auf dem Glas bemerkbar macht.

Bild 3.
Die Kathodenstrahlröhre im Betrieb, Röhrenspannung ca. 8500 V. Strahl und Leuchtfleck lassen sich durch einen in der Nähe befindlichen Magneten leicht ablenken. Man weist auf diese Weise auch nach, daß das gesamte Gebiet des negativen Glimmlichtes in einer Glimmentladung eigentlich Elektronenstrahl-Leuchten ist.

Nur zu ahnen ist im obigen Bild die Bildung gelblicher Ionenstrahlen vor der Kathode. Sie lassen sich mit der gleichen Röhre erzeugen, wenn die Elektroden umgepolt werden: dann ist ein honiggelber Ionenstrahl etwa 5 cm weit in den Kolben hinein zu beobachten. Als Vorversuch war das sehr aufschlußreich, denn schließlich sollen in einem Fusor ja später die Ionen den Weg bis zum Plasmafokus schaffen... mit der Kathodenstrahlröhre lassen sich also schon Untersuchungen zu den späteren Entladungsbedingungen machen.

Helium-Fusion?

Fast alle, die sich für Kernfusion interessieren, haben schon davon gehört, daß im Inneren unserer Sonne die Kernfusion von Wasserstoff zu Helium stattfindet. Die Sonne erzeugt auf diese Weise die gesamte Energie, die sie ausstrahlt.
Weniger bekannt ist, was passiert, wenn in einigen Milliarden Jahren der Wasserstoff im Zentrum der Sonne aufgebraucht ist. Die Fusion von Wasserstoff wird dann in einer Kugelschale um den ausgebrannten Heliumkern weitergehen. Während der Heliumkern sich zusammenzieht, dehnen die äußeren Schichten sich aus, die Sonne wird zu einem Roten Riesenstern. Irgendwann hat sich der Kern aus "Heliumasche" weit genug zusammengezogen und erhitzt, daß dort die nächste Stufe der Kernfusion beginnen kann: Helium beginnt zu Kohlenstoff zu fusionieren. Diese 3-Alpha-Reaktion erfolgt in mehreren Teilschritten:

	Schritt 1: ⁴He + ⁴He <--> ⁸Be
	Schritt 2: ⁸Be + ⁴He <--> ¹²C(*)
	Schritt 3: ¹²C(*) --> ¹²C + gamma

Hat sich erst einmal genug Kohlenstoff gebildet, kommt noch eine Nebenreaktion in Gang:

Schritt 4: ¹²C + ⁴He --> ¹⁶O + gamma

Aller Kohlenstoff und Sauerstoff im Universum, auch der unsere Körper und unsere Nahrung bildet und den wir einatmen, hat sich auf diese Weise in alten Sternen gebildet. Die Schritte 1 und 2 sind dabei Gleichgewichte, was bedeutet, daß sie auch rückwärts ablaufen können (der Stern am Kohlenstoffsymbol in Schritt 2 bedeutet, daß es sich um einen hochangeregten Atomkern handelt, der zu 99,9% wieder in Helium und Beryllium zerfällt und nur zu 0,1% nach Schritt 3 in stabilen Kohlenstoff übergeht).
Leider hat dieser Prozeß, der sehr schön auch in einem Fusor ablaufen könnte, einen Haken, und zwar das im Schritt 1 entstehende Berylliumisotop ⁸Be. Es ist derartig instabil, daß es nach nur 10^-16 Sekunden wieder in die beiden Heliumkerne auseinanderfliegt. Im Zentrum eines Sterns, in dem bei enormen Dichten eine gigantische Anzahl von Heliumkernen an der Reaktion teilnimmt, ist das kein Problem - es bildet sich trotzdem genügend ⁸Be, damit Schritt 2 und 3 in Gang kommen können, die stabilen Kohlenstoff (und Energie) liefern.
In einem Fusor ist die Situation leider nicht ganz so günstig, denn wir arbeiten dort mit einer Glimmentladung niedriger Dichte. Zwar kann Beryllium entstehen, doch ist die Wahrscheinlichkeit so gering, daß ausgerechnet in seiner kurzen Lebenszeit Schritt 2 der Reaktion abläuft, daß der Fusor mehrere Milliarden Jahre laufen müßte, um auch nur ein Kohlenstoffatom zu erzeugen.
Die Fusionsrate wird theoretisch üblicherweise berechnet durch

(Gleichung 1) r = n₁ * n₂ * sigma * v

wobei r, die Fusionsdichte, die Rate der Fusionen pro Sekunde und Kubikzentimeter bezeichnet, n₁ und n₂ die Teilchendichte der beiden Fusionspartner bezeichnet (meist in Teilchen pro Kubikzentimeter), v ihre relative Geschwindigkeit in Zentimeter pro Sekunde. Sigma ist der sogenannte Wechselwirkungsquerschnitt, eine Größe, die physikalisch die "Trefferfläche" beschreibt, die ein Teilchen für das andere bei der Geschwindigkeit v effektiv bereitstellt. Das Maß von Sigma ist deshalb auch das einer Fläche (in Quadratzentimeter), wobei man meist mit der Einheit Barn rechnet, die grob der Dimension des Atomkerns entspricht (1 Barn = 10^-24 cm²).
Schlägt man in Tabellen Werte von Sigma nach, so stellt man fest, daß die Zahlen meistens sehr klein sind. Hier drückt sich aus, daß sich Atomkerne wegen ihrer positiven Ladung stark abstoßen und keine besondere Neigung zum Verschmelzen haben; diese geringe Wahrscheinlichkeit geht in die Zahlenwerte von Sigma mit ein. Tatsächlich muß die Quantenmechanik hier mit dem Tunneleffekt zu Hilfe kommen, damit zwei Atomkerne sich überhaupt mit einer geringen Chance so nahe kommen, daß die Starke Kernkraft greift und die beiden Kerne trotz der Abstoßung verschmelzen.
Für technisch bedeutsame Fusionsreaktionen, etwa die Deuterium-Fusion oder die Deuterium-Tritium-Fusion, gibt es experimentell ermittelte Tabellen von Sigma, die man im Internet finden kann. Die Heliumfusion interessiert dagegen niemand - außer ein paar Astrophysikern, die sich mit theoretischen Sternmodellen beschäftigen. Man muß daher aus den astrophysikalischen Publikationen dieser Art die Berechnung von Sigma "extrahieren". Ich habe das für die obigen Schritte 1 und 2 getan (aus Referenzen [4,5]).

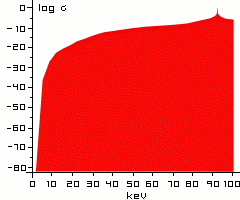Diagramm 1.
Log(sigma) der Reaktion ⁴He + ⁴He <--> ⁸Be zeigt aufgetragen über der Teilchenenergie den typischen logarithmischen "Elefantenbuckel" -Verlauf des nichtresonanten Anteils von Sigma, auf dem die kleine Spitze einer Resonanz sitzt. Im gezeigten Fall ist dies die Resonanz mit dem Grundzustand von ⁸Be.
Der Betrag von 91,78 keV entspricht genau der Energiedifferenz, die der ⁸Be- Grundzustand über dem Grundzustand von ⁴He liegt.
Eine Tabelle mit den Werten von Sigma im Textformat finden Sie HIER.

Berechnung der Fusionsrate

Im Fusor gibt es also nur auf Schritt 1 der 3-Alpha-Reaktion eine realistische Chance. Wir müssen uns daher mit der Frage beschäftigen, wieviele Kernfusionsreaktionen wir in einem Amateurfusor erwarten können. In der Praxis kann man Teilchendichte und -Fluß aus dem Druck im Fusor und der Stromstärke der Glimmentladung berechnen, die Beschleunigungsspannung liefert uns die Geschwindigkeit der Teilchen. Sigma bekommen wir aus einem Tabellenwerk (s.o.).
Mit den Werten von Sigma kann man sich also an eine überschlagsmäßige Berechnung machen. Es lohnt hierbei nicht, allzu genau zu sein, denn eine Menge physikalischer Effekte im Fusor werden durch das einfache Modell ohnehin nicht berücksichtigt. Beispielsweise können wir für den relativ hohen Druck von 13 Pa (0.1 Torr) die Rezirkulation von Ionen außer Acht lassen, da die freien Weglängen dafür nicht groß genug sein werden. Wir beschränken uns auf ein einfaches "ankommendes Ion trifft ruhendes Gasteilchen" (Modell 1) und werden alternativ "zwei ankommende Ionen treffen sich frontal" (Modell 2) untersuchen.

In einem Amateurfusor ist es praktischer, das Produkt n₂ * v aus Gleichung 1 durch eine Teilchenflußdichte f (in Teilchen pro Quadratzentimeter und Sekunde) zu ersetzen, die man direkt aus der Stromstärke der Glimmentladung ableiten kann:

(Gleichung 2) r = n₁ * f * sigma

Wir haben damit die Fusionsdichte in Fusionen pro Kubikzentimeter und Sekunde in einem Fusor. Um die absolute Rate in Fusionen pro Sekunde zu erhalten, müssen wir noch mit dem Volumen, in dem Fusionen stattfinden, multiplizieren und erhalten

(Gleichung 3) R = V * n₁ * f * sigma

Die Flußdichte f kann in absoluten Fluß F pro Fläche S aufgelöst werden:

(Gleichung 4) R = V * n₁ * F/S * sigma

Gehen wir nun davon aus, daß unser Fusor kugelsymmetrisch aufgebaut ist, so gilt V = 4/3 * pi * (d/2)³ und S = 4 * pi * (d/2)². Wir können folglich kürzen und erhalten:

(Gleichung 5) R = d/6 * n₁ * F * sigma

Diese Gleichung hat nun interessante Konsequenzen. Hängt die Teilchendichte n₁ von keiner anderen der beteiligten Größen mehr ab (was sie in Modell 1 nicht tut, denn die Teilchendichte der ruhenden Gasatome wird allein vom Druck bestimmt), dann steigt die Fusionsrate R linear mit dem Durchmesser d des betrachteten Gebietes an. Das macht auch Sinn, denn die ruhenden Heliumatome füllen ja den gesamten Raum aus. Ein ankommendes Ion kann schon in dem Moment, in dem es die Maschen des inneren Gitters durchfliegt, einen Stoßpartner finden. Man kann für Modell 1 also für d den Durchmesser des inneren Gitters wählen.

Berechnung von Modell 1
a) Berechnung der Teilchendichte: nach Avogadro's Regel nimmt 1 Mol jedes Gases bei Normalbedingungen 22,4 Liter Volumen ein. 1 Mol sind 6,022 * 10²³ Atome/Moleküle, pro Kubikzentimeter also 2,69 * 10¹⁹.
Im Fusor herrschen keine Normalbedingungen, sondern reduzierter Druck. Nach der Zustandsgleichung für ideale Gase sind Druck und Dichte einander proportional, wenn das Volumen und die Temperatur konstant bleiben (wir sollten im Hinterkopf behalten, daß das eine grobe Vereinfachung des Modells darstellt!). Bei 13 Pa (0,1 Torr) = 1/7600 Atmosphärendruck haben wir folglich noch n₁ = 3,5 * 10¹⁵ Teilchen in jedem Kubikzentimeter des Fusors.
Es schadet nicht, das mit der Dichte von Ionen zu vergleichen, die gerade den Plasmafokus durchfliegen, denn auch sie sind ja "da" und können als Stoßpartner dienen: gehen wir dazu von moderaten Bedingungen von 20 kV Beschleunigungsspannung und ca. 5 mA mittlerem Entladungsstrom aus (damit sind auch gepulste Entladungen abgedeckt, denn es dürfte praktisch sehr schwer werden, im Gleichstrombetrieb bei 0,1 Torr Druck die 20 kV bei 5 mA aufrechtzuerhalten - s.u.).
1 A entspricht einem Strom von 6,24 * 10¹⁸ Elementarladungen. Das Alpha-Teilchen oder He²⁺ - Ion trägt zwei davon, bei 5 mA sind also F = 1,56 * 10¹⁶ Ionen pro Sekunde in Richtung Plasmafokus unterwegs.
Die He²⁺ - Ionen haben bei einer Gitterspannung von 20 kV eine Energie von 40 keV entsprechend einer Geschwindigkeit von 1,4 * 10⁸ cm/s (übrigens fast 0,5% der Lichtgeschwindigkeit!). Setzt man für den Fusor ein kleines inneres Gitter (d = 2,5 cm) an, dann durchfliegt ein Ion das Gitter in nur 17,8 Nanosekunden. Von den 1,56 * 10¹⁶ Ionen, die pro Sekunde den Fokus erreichen, sind zu einem beliebigen festen Zeitpunkt also nur 8,7 * 10⁷ wirklich im inneren Gitter als Stoßpartner anwesend. Das ist verglichen mit dem Meer der neutralen Heliumatome vernachlässigbar.
b) Berechnung des Teilchenflusses: das haben wir im vorstehenden Absatz schon mit erledigt, denn wir hatten dort aus dem Strom von 5 mA schon ausgerechnet, daß 1,56 * 10¹⁶ Ionen pro Sekunde den Plasmafokus erreichen, folglich ist F = 1,56 * 10¹⁶ 1/s.
c) Sigma entnimmt man für eine Energie von 40 keV der Tabelle: rund 8,4 * 10^-12 Barn, das entspricht 8,4 * 10^-36 cm². Folglich können wir die Rate R berechnen:

R = d/6 * n₁ * F * sigma = 2,5 / 6 * 3,5 * 10¹⁵ * 1,56 * 10¹⁶ * 8,4 * 10^-36

= 1,9 * 10^-4 1/s

oder umgekehrt im Mittel etwa alle 5000 Sekunden (ca. eineinhalb Stunden) eine Reaktion / Bildung eines ⁸Be-Kernes.

Das, was einen Fusor interessant macht, ist ja gerade die Bildung des Plasmafokus im inneren Gitter. Offensichtlich füllt der aber nicht das gesamte innere Gitter aus. Die ankommenden Ionen konzentrieren sich offenbar erst weit innen so sehr, daß ihre Dichte merklich ansteigt. Berechnen wir die Anzahl der Ionen innerhalb einer Kugel mit dem Durchmesser d, so ist zunächst die Zeit, die das Ion braucht, um die Strecke d zu durchfliegen, t = d/v. Folglich ist

(Gleichung 6) n_d = F * t = F * d/v

die Zahl der Ionen, die sich als potentielle Ziele zu einem festen Zeitpunkt gerade in der Kugel mit dem Durchmesser d aufhalten. Man beachte, daß n_d die absolute Zahl der Teilchen ist, die nicht für n₁, eine Teilchendichte, in Gleichung 5 eingesetzt werden darf! Stattdessen ersetzen wir das Produkt V * n₁ aus Gleichung 4:

(Gleichung 7) R = n_d * F/S * sigma = F² * d/S * 1/v * sigma

Natürlich kann hier wieder die Kugelfläche gegen d gekürzt werden und wir erhalten:

(Gleichung 8) R = 1/(2*pi) * 1/d * F²/v * sigma

Diese Gleichung ist außerordentlich interessant, denn sie zeigt, daß die Fusionsrate aus Kollision der Ionen untereinander bei fester Beschleunigungsspannung umgekehrt proportional zum Durchmesser des Plasmafokus ist. Das zeigt sehr schön, daß eine sorgfältige Fokussierung des Fusors wichtig werden kann. Eine im Betrieb bedienbare Einstellmöglichkeit, vielleicht mit Hilfe von flexiblen Silikondichtungen für die Gitterträger, wäre wünschenswert.
Was aber noch bedeutsamer ist, ist die quadratische Abhängigkeit vom Teilchenfluß F, der direkt durch die Stromstärke gegeben ist. Starke Strompulse könnten hier also eine wesentlich bessere Ausnutzung der Energie als in einer Gleichstromentladung bedeuten. Wir kommen auf dieses Thema in einem der folgenden Abschnitte noch zurück.

Modell 2
a) Wir hatten beim Modell 1 schon berechnet, daß zu einem festen Zeitpunkt etwa 8,7 * 10⁷ Heliumionen im Fokus anwesend sind. Diese Ionen haben jedoch die unterschiedlichsten Bewegungsrichtungen, falls sie untereinander kollidieren, addieren sich die Geschwindigkeiten vektoriell. Um von einer Frontalkollision sprechen zu können, sollte der Kosinus des eingeschlossenen Winkels mindestens 0,86 oder mehr betragen (ca. 30 Grad oder weniger Abweichung von einer exakten Frontalkollision). Umgerechnet entspricht das einem Raumwinkel von 0,88 oder 7% der Vollkugel von 4*pi.
Von nur 7% von den zu einem festen Zeitpunkt im Fokus anwesenden Ionen kann man also erwarten, daß sie einem ankommenden Teilchen mehr oder weniger entgegenkommen, in Gleichung 8 muß also noch mit einem Faktor 0,07 multipliziert werden.
b) Für den Fall zweier sich entgegenkommenden Ionen müssen wir die Relativgeschwindigkeit ansetzen, für Sigma also den Tabellenwert von 80 keV benutzen. Das ist rund 3,5 * 10^-7 Barn (3,5 * 10^-31 cm²). Also ist in einem nicht allzu präzise fokussierten Fusor mit einem Plasmafokus von sagen wir 6 mm Durchmesser:

R_front = 0,07 * R = 0,07 * 1/(2*pi) * 1/d * F²/v * sigma

= 0,07 * 0,159 * (1,56 * 10¹⁶)²/(1,4 * 10⁸) * 1/0,6 * 3,5 * 10^-31

= 1,13 * 10^-8 1/s

was zunächst einmal sehr ernüchternd ist. Wir werden aber zu einem späteren Zeitpunkt im Zusammenhang mit gepulsten Entladungen diese Diskussion noch einmal aufgreifen.

Verbesserungen
Man kann natürlich versuchen, Strom und Spannung weiter aufzudrehen, um die Fusionsrate zu erhöhen. Das ist nur wenig sinnvoll, denn schon die Rechenbeispiele von 20 kV / 5 mA entsprechen einer Verlustleistung von 100 Watt, die aus dem Gefäß in Form von Wärme auch wieder abgeführt werden muß. Mehr Leistung stößt also sehr schnell an praktische Grenzen. Strompulse betrachten wir in einem folgenden Abschnitt noch.
Vielversprechender ist es dagegen, den Fokus zu verkleinern. Schafft man es, den Durchmesser des Plasmafokus von 6 mm auf 0,6 mm zu verkleinern, verzehnfacht sich die Fusionsrate. Damit berechnet sich R_front = 1,13 * 10^-7 1/s. Das ist immer noch nicht umwerfend, zeigt aber, in welche Richtung Verbesserungen eher laufen sollten.
Solche weitergehende Berechnungen der Reaktionen im Fokus eines Fusors und die Berechnung der Sigmas für die obigen Schritte 1 und 2 der 3-Alpha-Reaktion habe ich als C Programm erstellt, das Sie unter Download finden können.

Die Charge-Transfer-Schaltung

Ich hatte bei der Berechnung des obigen Beispiels schon angemerkt, daß die gewählten Werte von 20 kV und 5 mA bei einer Gleichstrom-Glimmentladung nur sehr schwer einzuhalten wären. Vakuum-Dioden haben eine ausgeprägte Strom-Spannungs-Charakteristik, die empfindlich vom Gasdruck abhängt, das weiß jeder, der schon mit Glimmröhren experimentiert hat. Im Prinzip bleibt zur Spannungsregelung nichts anderes übrig, als den Druck soweit zu erniedrigen, bis der Spannungsabfall über den Gittern einen akzeptablen Wert annimmt.
Strombegrenzung ist lebensnotwendig für das Netzteil und führt meist dazu, daß einfache Amateur- Fokusdioden nur bei gedrosselter Spannung betrieben werden können.
Eine solche Problematik läßt sich umgehen, wenn man zu gepulsten Entladungen übergeht. Damit meine ich nicht die Grobvariante, daß sich der Glättungselko des Netzteiles unkontrolliert durch den Fusor entladen darf (der speichert u.U. viele hundert Joule an Energie, was dazu führen kann, daß nach dem ersten Puls das innere Gitter fehlt). Ich spreche hier von Pulsgeneratoren, wie sie auch für Laser verwendet werden.
Eine ganze Reihe von Lasern benötigen kurze und sehr starke Pulse, um arbeiten zu können, insbesondere die selbstterminierten Laser. Oft muß die gesamte Anregungsenergie hier innerhalb weniger Nanosekunden eingebracht werden, bei Strömen, die im Kiloampere-Bereich liegen. Es gibt dafür geeignete Schaltungen: beim Stickstoff-Laser findet meist der Blümlein-Generator Anwendung, der wegen seiner Form für den Fusor aber eher ungeeignet ist. Geeigneter ist die Charge-Transfer-Schaltung, mir der wir uns unten beschäftigen wollen.
Einfache Kondensatorentladungen haben den Nachteil, daß nach der Zündung der Entladung die Spannung exponentiell abfällt. Selbiges tut auch der Strom, nachdem er einen Spitzenwert erreicht hat. Für einen Fusor ist dieses Verhalten denkbar ungeeignet, denn die Gitter sollen während des Pulses ja die volle Beschleunigungsspannung halten. Der Blümlein- und der Charge-Transfer- Generator leisten das. In beiden bleibt während des Pulses die Spannung weitgehend konstant oder steigt sogar leicht an, was zu enorm starken Strompulsen führt. Da die Energie des kurzen Pulses aber sehr beschränkt bleibt, hält sich die Belastung für die Elektroden dennoch in Grenzen.

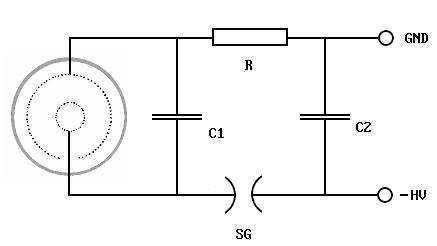Diagramm 1.
Schaltbild der Charge-Transfer-Schaltung. Sie besteht im Prinzip aus zwei gekoppelten LC-Schwingkreisen. C2 dient als Speicherkondensator, C1 ist der sogenannte "Peaker". Beide Kondensatoren müssen möglichst induktionsarm gebaut werden, C1 muß die doppelte Ladespannung aushalten können.
R trennt beide Kapazitäten voneinander. Die Funkenstrecke SG dient zur Schaltung des Pulses. Wird sie z.B. als regelbarer mechanischer Pulser ausgeführt, hat man eine leicht kontrollierbare Leistungsregelung der Schaltung.

Die Funktion der Charge-Transfer-Schaltung ist eigentlich recht einfach zu verstehen. Nachdem der Speicherkondensator C2 aufgeladen ist, wird die Funkenstrecke SG gezündet. C2 entlädt sich dann in C1, und beide Kreise schwingen mit einer Frequenz, die durch die Kapazitäten und die Induktivitäten der Leiterschleifen festgelegt ist. In der ersten Halbwelle addieren sich dabei die Amplituden, so daß bei geeigneter Wahl von C1 und C2 sogar eine Spannungsverdopplung erreichbar ist. Der begrenzende Faktor für die Stärke des sich einstellenden Entladungsstromes ist nur die Induktivität des Kreises.
In [6] wurde diese Schaltung eingehend untersucht, und ich gebe hier ein paar aus der Arbeit abgeleitete Gleichungen wieder, die für die Dimensionierung der Schaltung nützlich sind.
Definieren wir a = C1/C2 als das Verhältnis der Kapazitäten in der Schaltung, so ergeben sich die erreichbare Spitzenspannung über C1 und der Spitzenstrom zu

U_peak = 2 * U₀ / (1 + a)

I_peak = U₀ * omega * C_s

wobei U₀ die Ladespannung von C2 bedeutet, C_s die Gesamtkapazität im Kreis und omega die Kreisfrequenz, mit der die Schaltung schwingt. Diese Näherung gilt nur für den Fall, daß die Dämpfung vernachlässigbar ist (R ca. 10 Ohm) und die Induktivität möglichst klein. C_s berechnet sich aus 1/C_s = 1/C1 + 1/C2, und dann ist näherungsweise omega = 1/sqrt( L * C_s).
Die Induktivität L stellt ein Problem dar, denn sie ist normalerweise schwierig zu messen. Meist ist die Schaltung so ausgeführt, daß die Entladungsstrecke und C1 eine bauliche Einheit bilden, bei der die Induktivität vernachlässigbar klein ist. Der Ladekreis von C2 bestimmt dann L, und das sind gerade die Zuleitungen und Kabel. Bei den Experimenten mit dem Janus-Laser (siehe Diane's Laser Page) habe ich versucht, aus den erreichten meßbaren Parametern auf die Induktivität zurückzurechnen und bin auf die folgende grobe Daumenregel gekommen:

L = 100 * A [ uH ]

wenn A die von den Zuleitungskabeln eingeschlossene Fläche in Quadratmetern ist (das entspricht etwa der Formel für die Induktivität einer Luftspule mit einer Windung und 1 cm Länge). Also müssen die Kabel des Ladekreises möglichst kurz sein und möglichst ohne unnötige Schlaufen dicht beeinanderverlaufen.
Für den Anfang mag das als Dimensionierung genügen, langfristig ist es aber wünschenswert, mit Hilfe einer Stromsonde und eines Oszilloskops den Entladungsstrom direkt zu überwachen. Die Diagramme in Ref. [6] sind in dieser Hinsicht recht eindrucksvoll und zeigen, daß bei der ausgeführten Beispiel-Schaltung ein Strom von mehreren tausend Ampere während ca. 40 Nanosekunden floß. Die Spannung über C1 blieb dabei weitgehend konstant. Die Kürze des Pulses zeigt aber auch schon, daß es für den Fusor bestimmte Grenzen gibt. In einem Laser sollen die Pulse möglichst kurz sein. Die Ionen in einem Fusor müssen aber in der Lage sein, während des Pulses den Plasmafokus zu erreichen. Da wir oben schon festgestellt hatten, daß die Ionengeschwindigkeit etwa 0,5% der Lichtgeschwindigkeit beträgt oder 1,5 mm/nsec, dürfen bei großen Fusoren die Pulse nicht zu kurz werden. Generell sollte ein gepulster Fusor eher kleiner gebaut werden. Bei einem Radius des äußeren Gitters von 5 cm braucht ein Ion dann etwa 30 Nanosekunden bis zur Mitte.

Modell 3
Wir nehmen an dieser Stelle noch einmal das Ergebnis von Modell 2 auf und berechnen, welche Fusionsrate bei einem Einzelpuls mit der Charge-Transfer-Schaltung zu erwarten wäre. Wir nehmen einen nicht allzu starken Puls von 500 A mit einer Dauer von 100 ns an (das entspricht bei 10 pps einem mittleren Strom von 0,5 mA). Dann ist

R_front = 0,07 * 0,159 * (1,56 * 10²¹)²/(1,4 * 10⁸) * 1/0,6 * 3,5 * 10^-31

= 1,13 * 10² 1/s

Nun ist der Puls nicht eine Sekunde lang, sondern nur 100 ns, wir müssen also noch mit 10^-7 multiplizieren und erhalten R_front,puls = 1,13 * 10^-5 1/Puls.
Der gleichen Eingangsleistung wie in Modell 2 würde ein mittlerer Strom von 5 mA entsprechen, also 100 pps, was ein R = 1,13 * 10^-3 1/s ergibt - man vergleiche diese gepulste Fusionsrate mit der "Gleichstromrate" gleicher Eingangsleistung aus Modell 2!
Eine Reduzierung des Durchmessers des Plasmafokus auf 0,6 mm ergibt noch einmal wie oben einen Faktor 10, man ist dann bei 1,13 * 10^-2 Fusionen pro Sekunde (bei 100 pps) oder im Mittel alle 88 Sekunden eine Bildung eines ⁸Be - Kernes.
100 pps sind vielleicht ein bißchen optimistisch, und ein Fokusdurchmesser von 0,6 mm läßt sich sicher auch nicht ohne weiteres hinbekommen. Der Entladungsstrom dagegen kann sicher durch die o.a. Maßnahmen noch gesteigert werden... eine Fusion alle paar Minuten ist mit einer gepulsten Entladung offenbar nicht allzu utopisch.

P.S.
Auf welche Weise sich die "Produktivität" eines Deuterium-Fusors mit Hilfe einer gepulsten Entladung erhöht, überlasse ich der geneigten Leserin als Übungsaufgabe.

P.P.S
Bei den ersten praktischen Versuchen in Richtung gepulste Entladung hat sich leider aus ganz unerwarteter Richtung ein Problem ergeben, das mit der Ausführung der Gitter im Silmaril zusammenhängt und die obigen Berechnungen obsolet macht (siehe "Der Pulsar"). So geht's zuweilen mit der Theorie. Im folgenden Abschnitt führe ich deshalb noch ein paar Berechnungen zum Thema Niederdruck- Gleichstromentladung durch.

Fusionsrate bei niedrigem Druck

Na gut, mit Pulsen geht es nicht, also muß ich mit dem Silmaril wohl doch den Weg zu niedrigen Drücken einschlagen. Natürlich muß ich mein Vakuumsystem dazu aufstocken. Von einer Diffusionspumpe habe ich schon lange geträumt, und um ein Pirani- Vakuummeter komme ich dann wohl auch nicht herum. Immerhin, ich habe einen neuen Job, und habe ich bisher nicht immer das erste selbstverdiente Geld in eine Pumpe für mein Labor investiert...?

An dieser Stelle muß daher in die oben entwickelten Gleichungen für "Ion trifft ruhendes Gasatom" (Modell 1, Gleichung (5)) bzw. "2 Ionen prallen fast frontal aufeinander" (Modell 2, Gleichung (8)) noch eingebracht werden, was an Physik im Fusor bei sehr niedrigen Drücken zu wirken beginnt. Die Rede ist von der Rezirkulation der Ionen.
Rezirkulation wird wichtig, wenn die freie Weglänge der Ionen größer wird als der Durchmesser des Fusors. Die Ionen werden dann nach dem Durchfliegen des Plasmafokus auf der anderen Seite abgebremst, bis ihre Bewegungsrichtung sich umkehrt und sie wieder in Richtung Fokus beschleunigt werden. Einfache Modelle liefern die freie Weglänge eines Teilchen zu

(Gleichung 9) lambda = 1 / ( sqrt(2) * n₁ * pi * D² ) .

Interessant ist daran, daß lambda umgekehrt proportional zur Teilchendichte n₁ ist, unter Normalbedingungen also zum Druck. Alles andere, einschließlich dem Teilchendurchmesser D, sind Konstanten. Für Gase wie Luft erhält man so ungefähre freie Weglängen von lambda = 1 cm bei 133 Pa (1 Torr), lambda = 10 cm bei 13 Pa (0.1 Torr) etc. Sobald der Druck in einem Fusor niedrig genug ist, daß die freie Weglänge der Ionen größer wird als der Radius, beginnt sich in der Mitte der Plasmafokus auszubilden. Wird die freie Weglänge größer als drei Radien, beginnt die Rezirkulation sich bemerkbar zu machen. Bei noch niedrigeren Drücken können die Ionen im Prinzip so oft durch den Fokus hin- und hersausen, bis ihre freie Weglänge aufgebraucht ist oder sie auf einen Draht treffen.
Letzteres würde in Amateurfusoren die Rezirkulation üblicherweise auf weniger als 5 Durchläufe begrenzen, denn Drähte sind nun mal nicht unendlich dünn. Dennoch ist sie in vielen Fällen höher. Man beobachtet bei sehr präziser Ausrichtung der Gitter nämlich ein Phänomen, das von George Miley entdeckt wurde und allgemein als "Stern"-Modus bezeichnet wird. Die Ionen neigen dabei dazu, bevorzugt mitten durch die Maschen des inneren Gitters zu fliegen und die Drähte zu meiden (der Grund ist meines Wissens nicht genau bekannt). Dabei bilden sich sternartige Strahlen vom Fokus aus, die dem ganzen den Namen gegeben haben.
Bei einem Druck von 0.13 Pa (1 Micron, 0.001 Torr) hat man eine ungefähre freie Weglänge von 10 Metern, was bei einem Durchmesser des Fusors von 10 Zentimetern etwa 100 Durchläufen entspricht, wenn kein Draht getroffen wird. Solche Rezirkulations- Faktoren scheinen nach Richard Hull für sehr gut ausgeführte Amateurfusoren in der Tat erreichbar zu sein.
Bezeichnen wir den Rezirkulationsfaktor mit rho, dann wird der Teilchenfluß F aus Gleichung (5) und (8) nach kurzer Betriebszeit des Fusors bei Gleichstrom- Bedingungen sich durch die Rezirkulation vervielfacht haben. Konkret werden wir

(Gleichung 10) F' = rho * F

Teilchen pro Sekunde haben, die durch den Fokus zirkulieren.
Für höhere Drücke, wie sie bisher betrachtet wurden, ist natürlich rho = 1 und damit F' = F. Bei Einbeziehung der Rezirkulation geht Gleichung (5) über in

(Gleichung 11) R = d/6 * n₁ * rho * F * sigma.

Man muß dabei beachten, daß rho direkt proportional zur freien Weglänge lambda ist, also umgekehrt proportional zur Teilchendichte n₁. R bleibt in Modell 1 also unverändert, wenn wir Rezirkulation einbeziehen - gewissermaßen verlieren wir durch die verringerte Teilchendichte bei niedrigem Druck wieder, was wir an Rezirkulation gewinnen. Das Ergebnis verbessert sich nicht.
Hingegen ergibt sich für Gleichung (8) mit Rezirkulation

(Gleichung 12) R = 1/(2*pi) * 1/d * rho² * F²/v * sigma ,

der Rezirkulationsfaktor geht also quadratisch in R ein, während die Teilchendichte nicht mehr explizit in der Gleichung vorkommt. Gegenüber Modell 2 ist also für ein nicht allzu utopisches rho = 100 eine um den Faktor 10⁴ höhere Fusionsrate zu erwarten.
Verkleinert sich auch der Fokus bei sehr niedrigem Druck noch auf 0.6 mm, so ist ein Faktor 10⁵ erreichbar. Das entspricht für das modifizierte Modell 2' einer Fusionsrate von ungefähr R_front = 1.13 * 10^-3 1/s. Etwa alle 900 Sekunden eine Reaktion, das sind 15 Minuten.
Scheinbar ist es also auch ohne Pulse nicht ganz aussichtslos - wenn die Beschleunigungsspannung entsprechend gewählt wird, kann man sigma in die Nähe der Resonanzstelle bringen, wo der Wert um weitere Zehnerpotenzen ansteigt.
Die Grundidee ist die: die Resonanzenergie der Fusion zweier Heliumkerne liegt bei 91.78 keV, das entspricht also zwei Teilchen mit je einer Energie von 45.89 keV, die frontal aufeinanderprallen. Jeder Heliumkern trägt zwei Ladungen, erreicht die entsprechende Energie also nach dem Durchlaufen einer Spannungdifferenz von 22.95 kV.
Die Resonanz ist sehr schmal, sigma wird nur in einem etwa 200 eV breiten Bereich um die Resonanzstelle größer als 10^-2. Ob sich eine Gitterspannung von 23 kV so genau regeln und glätten läßt und ob die Teilchen wirklich so monoenergetisch sind, kann man nur noch raten - das hier entwickelte Modell liefert darauf keine Antwort mehr. Theoretisch läßt sich mit einem so hohen sigma eine Rate von etwa 100 Fusionen pro Sekunde berechnen.
Schaun wir mal, ob das praktisch machbar ist...

Fusion bei Resonanzenergie

Praktisch stellt sich als nächstes natürlich die Frage, was denn nun mit einer "verbrummten" Beschleunigungs- Spannung in dem oben diskutierten Fall ist. Wie ich eingangs schon erwähnte, bin ich ein bißchen faul und will nicht meine beiden alten und treuen Neon- Transformatoren wegwerfen. Also muß ich mir was einfallen lassen.
Hochspannung für Teilchenbeschleuniger wurde schon in den 1950er Jahren ganz gern mit Kaskadengeneratoren erzeugt (siehe [7], Kap. II). Leider haben gerade Kaskadengeneratoren das Problem, daß durch das Umladen der Kondensatoren in den verschiedenen Stufen nicht wenig Brummspannung erzeugt wird. Eine Abschätzung mit den Näherungsformeln nach [7] für einen selbstgebauten 3-stufigen Generator mit Speisespannung 5,6 kV und Leerlaufspannung 33,6 kV würde beispielsweise bei einer Belastung von 5 mA, wie wir sie oben stets angenommen haben, einen (Gleich-) Spannungsabfall in der Kaskade von 10,6 kV ergeben (damit ist die Netto- Ausgangsspannung gerade 23 kV). Zusätzlich errechnet sich die Brummspannung in diesem Fall zu rund 3 kV.
Das ist nicht wenig. Kann man ein gewissermaßer für diesen Bereich "gemitteltes" sigma berechnen? Wenn die Gitterspannung im Fusor nämlich mit 23 +/- 1,5 Kilovolt vor sich hinbrummt, werden doch die Teilchen mit allen möglichen Spannungen in diesem Bereich beschleunigt, je nach momentaner Phasenlage der Brummspannung. Frontale Kollisionen von Heliumkernen werden also mit allen möglichen Energien im Bereich 92 +/- 6 keV stattfinden.
Das führt natürlich auf den Gedanken, sigma einfach zu mitteln. Bedingt durch die Tatsache, daß sigma unter 90 keV und über 94 keV vernachlässigbar klein ist, wenn man aufsummiert, spielt die genaue Lage der Grenzen dabei für die Näherung keine Rolle. Das numerische Integral über den Resonanzpeak errechnet sich so zu ungefähr 0,1573 barn * keV, wenn die Integration den Peak grob (um ein paar Kiloelektronenvolt) einschließt. (Diesen Wert habe ich mit Hilfe eines der oben für die Berechnung von sigma angegebenen C-Programme errechnet, das für die Integration etwas erweitert wurde.)
Den Mittelwert von sigma findet man dann, indem man den Integralwert durch die Breite des Energieintervalls der Heliumkerne teilt. In unserem Fall der Frontalkollision zweier Kerne ist das jeweils 4 mal der Brummspannung (jeder Kern hat zwei Ladungen, und die Relativ- Geschwindigkeit ist bei Frontalkollision doppelt so groß wie die Geschwindigkeit beider Kerne). Also ist

(Gleichung 13) sigma_mittel,92keV = 0.1573 / ( 4 * U_Brumm[keV] ) barn

eine vertretbare Näherung für ein mittleres sigma, wenn der Fusor mit einer Gitterspannung so betrieben wird, daß die Resonanzenergie innerhalb des "Brummens" der auftretenden Teilchenenergien liegt. Im oben diskutierten Beispiel für eine Kaskade mit einer Brummspannung von 3 kV wäre sigma also ungefähr im Mittel 1,3 * 10^-2 barn oder 1,3 * 10^-26 1/cm².
Eine solche Mittelung bedeutet fast schon Thermalisierung, und ehrlich gesagt passiert das unbeabsichtigt sicher in fast jedem Amateurfusor. Wer von uns kann sich schon ein vernünftig gefiltertes Hochspannungs- Netzteil leisten oder bauen...?
Die gemittelten sigma-Werte werden jetzt erfreulich groß, so daß wir vielleicht noch ohne die extremen Rezirkulationen im Sternmodus auskommen - ich verlasse mich lieber erstmal nicht darauf, daß ich den Silmaril dafür wirklich präzise genug gebaut habe. Die mechanische Stabilität meiner Fokussierhilfe mit den drei Plastikschrauben ist noch nicht bewiesen. Rho wird also zunächst einmal als geometrische Rezirkulation angesetzt, die für eine "Transparenz" T des inneren Gitters gerade

(Gleichung 14) rho = 1 / ( 1 - T )

wird. Ein Gitter von 90% Transparenz (T = 0,9), vertretbar für Amateur- Bauweise mit dünnem Draht, ergibt also gerade rho = 10. Für die Fusionsrate bedeutet das näherungsweise, angewandt auf Gleichung (12) und die obige Beispiel-Kaskade

R_{front,resonanz} = 0,07 * 1/(2*pi) * 1/d * rho² * F²/v * sigma_mittel,92keV

= 0,07 * 0,159 * 10² * (1,56 * 10¹⁶)²/(1,4 * 10⁸) * 1/0,6 * 1,3 * 10^-26

= 4,2 * 10^-2 1/s

oder alle 23.8 Sekunden eine Reaktion. Das klingt doch schon ganz vernünftig. Für den Fall, daß die extremen Rezirkulationen des Sternmodus einbezogen werden, etwa für rho = 100, steigt die Rate noch einmal um den Faktor 100 an und wir wären bei rund 4 Bildungen von ⁸Be-Kernen pro Sekunde.

P.S. Diese Überlegungen lassen sich leider nicht in analoger Weise für einen Deuterium- Fusor durchführen. Die Resonanz der D+D- Reaktion liegt viel zu hoch (sigma hat einen sehr breiten Resonanzpeak um etwa 2,5 MeV [+/- 2 MeV]) - Amateure sind hier dazu verdammt, im nichtresonanten Bereich zu bleiben.

Strahlungsbelastung durch einen Fusor

Ein Fusor erzeugt drei Arten von Strahlung, die für die Umwelt gefährlich sein können, nämlich Ultraviolettstrahlung, Röntgenbremsstrahlung und im Fall des Deuterium-Fusors auch noch Neutronenstrahlung. Diese drei Arten lassen sich unterschiedlich schwer abschirmen.
UV-Strahlung bekommt man am einfachsten in den Griff, weil die meisten Gläser und natürlich Metall nicht für sie durchlässig sind. Manche Plastiksorten sind für sie durchlässig, deshalb noch einmal die Warnung vor billigen Exsikkatoren als Kammer für den Fusor! Wasserstoff, Helium und auch andere Gase haben eine Reihe sehr starker Spektrallinien im UV, die von der Glimmentladung in einem Fusor auch emittiert werden.
Röntgen-Bremsstrahlung hängt in ihrer Gefährlichkeit sehr von der Gitterspannung ab. Glas wird erst oberhalb von 20 keV von Röntgenstrahlen durchdrungen, Metall bietet hier naturgemäß mehr Schutz. Bei mehrfach geladenen Ionen ist die kinetische Energie ein Mehrfaches der Gitterspannung (kV) in keV, das muß berücksichtigt werden.
Neutronenstrahlung ist naturgemäß am gefährlichsten. Weder Glas noch Metall bieten Schutz. Abschirmung ist möglich durch eine dicke Schicht Wasser, Holz oder Paraffin, gefolgt von einer Schicht Bor, gefolgt von einem Bleiblech.

Neutronen
Auch wenn der Helium-Fusor keine Neutronen erzeugt, ist es trotzdem interessant zu wissen, ab wann man aufpassen müßte.
In Deutschland ist die gesetzliche Vorgabe für Personen, die beruflich mit Strahlung zu tun haben, eine Dosisleistung von 20 uSv/h, wenn die Belastung an nicht mehr als 250 Stunden pro Jahr erfolgt (ein Amateur-Fusor müßte dazu an 5 Tagen pro Woche eine Stunde in Betrieb sein - etwas übertrieben für ein Hobby!)
Die Dosisleistung in Sievert (Sv) hängt mit der Energiedosisleistung in Gray (Gy) über einen Gewichtungsfaktor q zusammen. Wir verwenden hier den von der EU-Kommission empfohlenen strengeren Faktor von q = 20. Demnach dürfte der Fusor höchstens 1 uGy/h = 10^-6 J/kg /h in Form von Neutronenstrahlung erzeugen.
Wir nehmen hier einen sehr unvernünftigen Experimentator an, der seinen Lieblings-Fusor im Betrieb immer im Arm hält, so daß sein Körper alle Neutronen abbekommt. Bei einem Körpergewicht von 70 kg für eine erwachsene Person dürfte die Energie aus Neutronenstrahlung dann höchstens 7 * 10^-5 J/h betragen oder 1,9 * 10^-8 J/s.
Neutronen aus der Deuterium-Fusion haben eine Energie von rund 3 MeV oder 3,16 * 10^-13 J. Dividiert man, so erhält man eine höchstzulässige Neutronen-Produktion von 60.000 Neutronen pro Sekunde.
Wohlgemerkt, das ist die absolute Obergrenze, bei der man keiner anderen Belastung ausgesetzt sein darf und tunlichst keine Krebsvorsorgeuntersuchung verpassen sollte (wie das bei beruflich strahlenbelasteten Personen ja wohl auch Vorschrift ist).
Zwar geht die Belastung zurück, wenn der Abstand vergrößert wird (s.u.), aber man sollte nicht vergessen, daß auch in 1 m Abstand der Körper in diesem Fall immer noch von tausenden von Neutronen pro Sekunde durchsiebt wird. Von dem Wasser des Körpers abgebremst (man sagt auch: moderiert), können sie von Atomkernen im Körper eingefangen werden und künstliche Radioisotope bilden. Diese zerfallen dann ihrerseits, und da sie sich im Körper befinden, gibt es absolut keinen Schutz gegen die so induzierte Sekundärstrahlung.

Röntgenstrahlung
Bei einem Fusor aus Metall braucht man sich bis zu ziemlich hohen Gitterspannungen keine Gedanken um dieses Thema machen. Ist das Gefäß jedoch aus Glas (oder enthält Fenster aus Glas), dann wird es bei Spannungen über 20 kV gefährlich, da dann die Röntgenbremsstrahlung das Glas durchdringen kann.
Röntgenbremsstrahlung kann auf zwei Arten entstehen: einmal durch die Elektronen, die vom inneren Gitter zum äußeren fliegen und auf die Kammerwand prallen. Zum zweiten entsteht Röntgenstrahlung auch durch die Ionen, die im Plasmafokus zusammenprallen und dabei abgebremst werden.
Kehren wir noch einmal zu dem Rechenbeispiel aus einem der vorigen Abschnitte zurück, so ist auch ein Helium-Fusor aus Glas bei 20 kV nicht unbedingt "sicher", sondern man muß berechnen, wieviel Röntgen-Bremsstrahlung durch 40-keV-Ionen entstehen kann.
Wir gehen dabei von dem Idealfall aus, daß die gesamte Leistung in Bewegungsenergie von Heliumionen und Elektronen umgesetzt wird. Da ein neutrales Heliumatom in 2 Elektronen (zu je 20 keV) und den Kern (zu 40 keV) zerlegt werden kann, verteilt sich die Leistung etwa zur Hälfte auf Elektronen und Ionen. Das wären dann 50 J/s für die Heliumionen. Glücklicherweise ist der Wirkungsgrad bei der Erzeugung von Röntgenstrahlen sehr klein (ca. 10^-9), so daß etwa 5 * 10^-8 J/s an 40-keV-Röntgenstrahlen erzeugt werden. Durch eine 3-mm-Glaswand gehen ca. 2/3 davon hindurch, so daß etwa 3,3 * 10^-8
J/s außerhalb des Fusors freigesetzt werden.
Gehen wir zunächst einmal wieder von dem unvernünftigen Experimentator aus, der alle Strahlung mit seinem Körper auffängt, so entspricht das einer Energiedosis von 4,7 * 10^-9 J/kg /s oder 1,68 * 10^-5 J/kg /h = 16,8 uGy/h.
Für q = 1 entspricht das also rund 17 uSv/h, für den hier angenommenen allerungünstigsten Fall also noch innerhalb des o.a. gesetzlichen Rahmens.
Nun wird niemand so verrückt sein, einen laufenden Fusor im Arm zu halten. In einem Meter Abstand verringert sich die Belastung bei einer normal großen Person (sagen wir 1,80 groß und 0,60 breit) auf etwa 8,5% davon, wenn man die Fläche in Beziehung zur Vollkugel setzt. Das wären dann noch 1,4 uSv/h - auch hier gilt, daß es keine ungefährliche Dosis gibt. Zudem ist die obige Abschätzung für den denkbar schlechtesten Fall durchgeführt - in der Praxis wird nicht 100% der Energie in die Bildung von voll ionisiertem Helium umgesetzt, und auch die Röntgenstrahlung wird nicht nur aus 40-keV-Photonen bestehen, sondern ein breites Spektrum weicherer Strahlung enthalten, die vom Glas besser geblockt wird.
Trotzdem, ein größerer Abstand oder eine Abschirmung aus Metall kann in diesem Fall sicher nicht schaden, und auch nicht, ein Strahlungsmeßgerät bereitzuhalten, um zu kontrollieren, wieviel Röntgenstrahlung in der Praxis denn tatsächlich erzeugt wird.

Teil II: Experiment - der SILMARIL

Die Vakuumkammer

Bild 1.
Die Teile der Vakuumkammer stammen aus dem Laborhandel. Zwei Deckel gewöhnlicher Planflansch-Reaktoren aus Duranglas mit der geeigneten Anzahl von Schliffen bilden die Hälften der Kammer. Ebenfalls Standard-Bauteile sind die Übergänge von den 29/32 Normschliffen auf GL18-Klemmverschraubungen.
Die Glasteile werden durch passende Edelstahlklammern zusammengehalten.

Für den Bau einer Vakuumkammer für Fusor-Experimente finde ich die Teile aus dem Laborhandel sehr geeignet, auch wenn sie nicht ganz billig sind. Zum einen sind nämlich Planflanschreaktoren für Experimente bei Vakuum und hohem Druck vorgesehen, bestehen daher aus sehr dickem Glas und sind entsprechend stabil. Zum anderen sind die genormten Schliff-Verbindungen ein wahrer Baukasten, mit dem sich die unterschiedlichsten Kammer-Anordnungen herstellen lassen. Raum für spätere Veränderungen bleibt also genug. Nicht zu vergessen, daß Schliffe mit dem geeigneten Fett quasi selbstverständlich vakuumdicht sind.

Bild 2.
Der Aufbau mit der zusammengesetzten Kammer. Wegen ihrer komplett gläsernen Erscheinungsform nenne ich sie den "Silmaril" -- Sie dürfen raten, wer zu meinen Lieblingsautoren zählt... ;)
Bei den ersten Tests war nur die Hilfskathode in Betrieb (das lang herausstehende Glasrohr links vor der Vakuumpumpe), um das Prinzip der Druckmessung auszuprobieren. Die Hauptkathode (inneres Gitter) fehlt noch, der entsprechende Anschluß ist durch einen Blindstopfen abgedichtet (rote Schraubkappe).

Die Elektroden- und die Pumpanschlüsse sind aus 10mm- Duranrohr und Metall hergestellt. Die Übergänge sind dabei mit Epoxydharz verklebt, eine Technik, die sich schon beim Bau von Laserröhren bewährt hat.
Das Anodengitter ist aus Kupferdraht hartgelötet und mittels einer passenden Hülse auf eine Gewindestange in dem Duranrohr aufgeschraubt.
Verglichen mit anderen Amateur-Fusoren ist der Silmaril relativ klein: die Kammer besitzt einen DN100- Flansch, und das Anodengitter hat dementsprechend einen Durchmesser von nur 9 cm. Hier spielt eine Rolle, daß später Pulsexperimente folgen sollten, aber auch ganz profan das Geld. Größere Deckel sind sehr viel teurer.

Bild 3.
Die Hilfskathode in Betrieb, für diesen Test befand sich noch Luft in der Kammer. Das ausgedehnte negative Glimmlicht ist links sehr schön zu erkennen, rechts im Schliff erkennt man noch einen Teil der positiven Säule, ehe die Entladung in der Kammer zerfasert. Die Fluoreszenz von Elektronenstrahlen ist ebenfalls zu erkennen.
Zur Begrenzung des Entladungsstromes ist vor die Hilfskathode ein 1 MegaOhm / 200W - Widerstand geschaltet.

Leider ist auch auf Bild 3 wieder die Bildung eines rosafarbenen Ionenstrahls direkt vor der Hilfskathode schlecht zu erkennen - da wo sich auf dem Bild ganz links die Entladung einzuschnüren scheint, ist der Kathoden-Dunkelraum. Er ist bei diesem Experiment etwa 11 mm lang, was leicht direkt am Rohr mit Hilfe einer Schiebelehre oder einem Lineal gemessen werden kann. In Luft entspricht das einem Druck von 12 Pa (0.09 Torr, 90 Micron).
Ich habe ein bißchen mit dem Nadelventil herumgespielt, um zu testen, wie gut sich der Druck im Durchfluß regeln läßt. Es zeigte sich, daß sich bei laufender Pumpe bis ca. 20 Pa (0.15 Torr) noch ein stabiler Gasfluß einstellen läßt. Darunter ist es ein bißchen ein Glücksspiel.
Das negative Glimmlicht an der Hilfskathode bietet übrigens noch einen weiteren Vorteil: es führt gewissermaßen automatisch eine spektroskopische Analyse des Kammerinhaltes durch. Mit einem kleinen Spektroskop lassen sich die charakteristischen Linien des Gases und der Verunreinigungen erkennen. Auf diese Weise lassen sich in Luft Spuren von Wasserstoff (vermutlich aus Feuchtigkeit) und Kohlenstoff (vermutlich rückdiffundiertes Öl aus der Pumpe) sowie etwas Quecksilber aus dem Barometer nachweisen. Bei Durchflußbetrieb werden die Spektrallinien der Verunreinigungen schwächer - die Grenze des Machbaren scheint hier auch so in der Größenordnung von 13 Pa (0.1 Torr, 100 Micron) zu liegen. Darunter befindet sich fast nur noch Dreck in der Kammer.
Ich muß noch Versuche mit langer Laufzeit durchführen, um herauszufinden, ob dieses Verhalten sich nach längerer Zeit unter Vakuum noch verbessert. Allerdings wird das kaum eine Rolle für praktische Versuche spielen - genau wie bei den Lasern habe ich nämlich keine Lust, nach dem Aufbau tagelang zu pumpen, ehe ich anfangen kann mit dem Silmaril zu arbeiten.
Nachtrag: inzwischen habe ich eine Öldiffusionspumpe, mit der das natürlich wieder ganz anders aussieht...

Die Gitter

Nachdem sich herausgestellt hatte, daß mein Konzept der Druckmessung mit einer Hilfskathode ganz gut funktioniert, war der nächste Schritt natürlich die Installation des inneren Gitters und seines Halters. Hier habe ich die Materialkombination Quarz/ Edelstahl gewählt, weil sich diese Materialien einfach beschaffen und bearbeiten lassen und bis 1500 Grad belastbar sind.
Wie weiter oben schon beschrieben, sollte der innere Gitteraufbau zudem in irgend einer Weise justierbar sein - eine Unterstützung durch drei Schrauben, ähnlich wie bei dem Spiegelträger eines Lasers, bot sich hier an. Bei der Nähe zur Hochspannung muß so etwas natürlich aus isolierenden Materialien bestehen, denn eine Fokussiereinheit, die man im Betrieb zum Nachstellen nicht anfassen kann, ist ziemlich nutzlos (für mich).

Bild 1.
Die fertige Kammer des Silmaril, einzeln photographiert. Man erkennt links lang herausstehend die Hilfskathode, den kurzen Anodenanschluß und die beiden Messingoliven für Pumpe und Gaszuführung. Rechts ragt der Kathodenanschluß aus der Kammer. Mit Hilfe der drei weißen Kunststoff- Schrauben läßt sich das (innere) Kathodengitter innerhalb des (äußeren) Anodengitters positionieren (das funktioniert sogar während des Betriebes). Die Idee dazu stammt von einem Laser- Spiegelträger.

Bild 2.
Blick in die Kathodenhälfte der geöffneten Kammer mit dem inneren Gitter und seinem Träger.
Das Gitter besteht aus 0,8 mm Edelstahldraht und ist (in Variation der ursprünglichen Idee der Spiralkathode von Gerardo Meiro) aus einem Stück zu einer Doppelspirale gebogen. Es wird mit zwei Edelstahlmuttern auf einem Edelstahl- Gewindestab gehalten, der von einem Quarzrohr umgeben ist. Dieser Aufbau sollte bis zur Gelbglut eigentlich keine mechanischen Probleme bereiten.
Der Durchmesser des inneren Gitters beträgt 20 mm.

Bild 3.
Das Gegenstück: aus 1,5 mm Kupferdraht hartgelötete Anoden- Gitterkugel in ihrer Kammerhälfte. Auch sie ist auf einen Edelstahl- Gewindestab geschraubt, der allerdings nur von einem Duranglasrohr umgeben ist. Durchmesser des äußeren Gitters 90 mm.

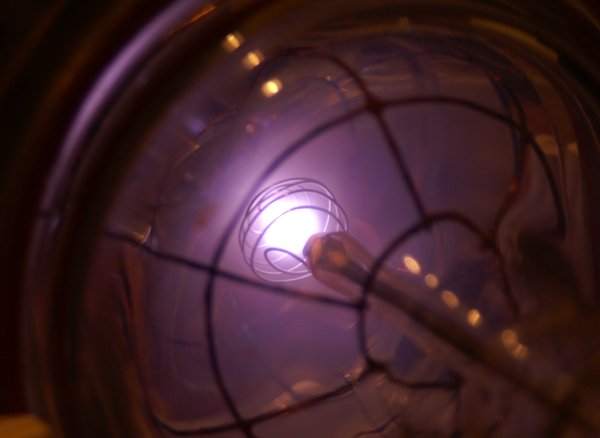
Die ersten Versuche mit der kompletten Kammer habe ich wieder nur mit der Hilfskathode gemacht - ich wollte schlichtweg wissen, ob die Dichtung am Quarzrohr (dem Träger des inneren Gitters) auch dicht bleibt, wenn man unter Vakuum an den Schrauben der Fokussiereinheit herumdreht. Das funktioniert ganz gut. Das Gitter läßt sich so in einem relativ weiten Bereich der Kammermitte hin- und herschieben, ohne Luft einzulassen.
Natürlich hat mich an diesem Punkt, mit einem benutzbaren inneren Gitter, sehr interessiert, ob der Silmaril schon als Fokusdiode arbeitet, und ich habe dazu den Spannungsanschluß mit dem Vorwiderstand von der Hilfs- auf die Hauptkathode umgesteckt. Es ergab sich ein faszinierender Anblick:

Bild 4.
Blick durch das Kathodenende der Kammer auf das innere Gitter, Gleichstrombetrieb. Wie bei meinen Lasern wird frisches Gas kontinuierlich durchgepumpt. Bei 40 Pa (0,3 Torr, 300 Micron) Heliumdruck bildet sich ein Plasmafokus (Poissor) mit einem Durchmesser von ungefähr 10 mm. Wegen des hohen Vorwiderstandes (Strombegrenzung) beträgt die Spannungsdifferenz über den Gittern hier nur etwa 500 V.

Bild 5.
Gleiche Bedingungen wie oben, durch die Seitenwand der Kammer gesehen und mit etwas kürzerer Belichtung aufgenommen. Der transparente Charakter des Plasmafokus wird so deutlicher. Sehr schön auch zu sehen der kelchförmige Elektronenstrahl, der aus der Mitte ausgeworfen wird.
Auf dem Photo leider nicht zu erkennen ist eine gelbliche "Korona" von rekombinierendem atomaren Stickstoff, die den Fokus umgibt. Stammt wohl aus Luftverunreinigungen, das Bandenspektrum ließ sich mit meinem neuen Spektroskop später deutlich beobachten.

Mit einem kleinen Handspektroskop beobachtet man im Plasmafokus recht kräftige Linien von He und He⁺ - wobei man letzteres am besten an der hellgrünen Linie bei 541 nm sieht, denn die beiden He⁺-Linien bei 656 und 486 nm lassen sich mit Amateurmitteln nicht von denen von Wasserstoff aus Verunreinigungen unterscheiden. Man "ahnt" lediglich, daß 486 nm durch He⁺ stärker aussieht als in einer Wasserstoffentladung, denn in Helium liegen hier in Wirklichkeit zwei Linien bei 486.6 und 485.9 nm dicht beeinander.
Spektroskopisch bemerkt man auch, daß Verunreinigungen bei niedrigeren Drücken als 32 Pa (0.25 Torr) eine immer größere Rolle spielen; der Untergrund wird stärker, die Linien verwaschener, bis schließlich die Stickstoffbanden von Luft, Halpha und die Kohlenstofflinien das Spektrum dominieren und die Heliumlinien eher schwach erscheinen. An der Hilfskathode trat dies nicht so deutlich in Erscheinung, und interessanterweise macht es sich auch am Plasmafokus äußerlich kaum bemerkbar, er ändert seine Gestalt nicht, wenn die Gaszusammensetzung verändert wird. Auch der Spannungsabfall über den Gittern verändert sich kaum. Lediglich die Farbe wechselt von einem ganz leicht grünstichigen Blauweiß (für reines He) zu einem violettstichigen Weiß (hoher Luftanteil). Der ausgeworfene Elektronenstrahl ist in Helium leicht rosa, in Luft eher weißlich.

Der "Pulsar"

Vielleicht wird es niemand überraschen, daß ich das Zubehör für die gepulste Fusor-Entladung auch wieder modular aufgebaut habe. Namentlich die Kombination Speicherkondensator und Funkenstrecke, die ja einen Teil der Charge-Transfer-Schaltung bilden, kann man schön in einer Kiste unterbringen und auch noch für andere Experimente verwenden.
Von besonderem Interesse ist dabei die Ausbildung der Funkenstrecke als mechanischer Pulsschalter. Solche Geräte sind verschiedentlich in Amateur- Metalldampflasern verwendet worden. Ein solcher Pulsschalter besteht aus einem sich propellerartig drehenden Metallstab, der in horizontaler Lage zwei Kontakte fast berührt (in diesen Momenten entsteht ein Funkenüberschlag). Gelagert ist der Metallstab auf einer langen isolierenden Achse aus Glasfaser, die dadurch gefahrlos von einem kleinen Niederspannungs- Getriebemotor angetrieben werden kann. Die Umdrehungszahl und damit die Pulsfolgefrequenz kann so einfach über die Spannung des Motors geregelt werden.

Bild 1.
Kondensatoren und Pulsschalter in einem Gehäuse. Ganz rechts der Regelknopf für die Motorspannung. Am linken Ende befindet sich der Hochspannungsteil. Ein 40 nF und ein 20 nF Kondensator (Polystyrolplatten/ Aluminium) können über dick isolierte rote Stecker zugeschaltet werden, so daß drei Konfigurationen für den Kondensator möglich sind. Die Pulsfrequenz läßt sich kontrolliert von 2-16 Hz regeln.
Wegen des schnarrenden Geräusches im Betrieb, das an die Namensvettern aus der Radio- Astronomie erinnert, nenne ich ihn den "Pulsar".

Im Testbetrieb ergaben sich allerdings ein paar Probleme. Die oben angegebene Schaltung für Charge-Transfer funktioniert zwar wunderbar für einen Laser wie Janus mit seiner langen dünnen Kapillare, aber nicht für ein dickes kurzes Gefäß wie den Fusor. Beim Zünden der Funkenstrecke brennt die meiste Zeit über ein Gleichstrombogen, weil der Spannungsabfall in der Röhre viel zu klein ist, um ihn wieder abreißen zu lassen.
Folglich mußte ich die Schaltung so verändern, daß sie gleichstrommäßig von der Spannungsversorgung abgetrennt ist, wenn die Funkenstrecken zünden. So verändert, läßt sich über die Steuerung der Pulsfolge die Energie, die in die Röhre eingebracht wird, genau steuern. Ein Teil bleibt dabei natürlich als Verlust in den Ladewiderständen hängen, aber ich kann mit dem Pulsar bis zu 52 Watt (60 nF @ 10kV, 16 Hz) kontrolliert in ein Experiment einbringen.
Mit den kleineren Kondensatoreinstellungen (20 nF, 40 nF) ist die Abhängigkeit der Leistung von der Pulsfrequenz sogar im Rahmen der Meßgenauigkeit linear. Bei 60 nF fällt sie oberhalb von 10 Hz etwas unter die Linearität, ich vermute mal, daß der Trafo hier die Spitzen der Nachladeströme für die Kondensatoren im Spannungsverdoppler nicht mehr ganz liefert, weil die Kerndrosselung greift. Ein zweiter Trafo parallel sollte das Problem aber lösen....

Natürlich hab ich auch schon mal probiert, was der Pulsar denn am Silmaril so macht. Das Resultat sind heftige Funken an den Elektroden, wie sie auch an nicht gut funktionierenden Stickstofflasern beobachtet werden können, und die eines deutlich anzeigen: aufgrund der zu langen Pulse destabilisiert die anfängliche Glimmentladung und bildet Bogenentladungen aus. Der Grund dafür sind bei Lasern (1) zu hohe Induktivität - kein Wunder bei so langen Kabeln am Silmaril (und dazu noch der spiralförmigen Kathode), oder (2) zu hoher Gasdruck. Letzteres muß noch weiter untersucht werden.
Zum Thema Induktivität muß ich noch anmerken, daß im Moment natürlich noch der "Peaker" Kondensator in der Schaltung fehlt, der für die kurzen Pulse mit doppelter Ladespannung sorgen soll.

Addendum: einige Monate später habe ich bei einer genaueren Untersuchung des Silmaril noch ein weiteres Problem entdeckt: an der Glaswand finden sich zum Teil massive Ablagerungen. Ursprünglich Kupfer von der Anode, bestehen sie inzwischen aus Kupferoxid.
Eigentlich kein Wunder, denn eine Kondensatorentladung führt ja starke Strom- Schwingungen aus. Für eine kurze Zeit war der Silmaril während jeder Schwingungsperiode also umgekehrt gepolt, das äußere Kupfergitter wurde die Kathode. Offensichtlich trat dabei starke Kathodenzerstäubung auf ("Sputtern").
Das Fazit ist also, daß der Silmaril mit der gegenwärtigen Elektrodenausführung nicht gut für gepulste Entladungen geeignet ist. Schade um die schöne Theorie...

Vorbereitung des Niederdruck-Betriebes

Wie schon im theoretischen Abschnitt angekündigt, habe ich nach dem Fehlschlag des Pulsar-Experimentes doch in Richtung einer Niederdruck- Gleichstrom- Entladung geplant. Mit meinem Vakuumsystem ist es nämlich nicht so ohne weiteres möglich gewesen, in diesen Bereich vorzustoßen. Nicht einmal das Potential meiner einstufigen Vakuumpumpe konnte ich damit voll ausschöpfen, wie sich gezeigt hat.
Zwei Problemkreise sind bei niedrigem Druck sehr wichtig: der Durchmesser der Leitungen muß groß genug sein, da die freie Weglänge der Moleküle mit sinkendem Druck immer größer wird. Makroskopisch äußert sich das in steigender Viskosität. Man kann sich das also anschaulich so vorstellen, als muß die Pumpe Honig durch ein Rohr saugen: bei einem dünnen Strohhalm klappt das nicht gut. Als erstes mußte also ein hochvakuumtauglicher Metallschlauch und ein passender Hahn her.
Zweitens ist mein improvisiertes Hilfskathoden- Meßgerät für niedrigere Drücke als 13 Pa (0.1 Torr) kaum noch zu gebrauchen. Da mußte etwas besseres her, und ich entschied mich, das Geld für ein Pirani- Vakuummeter zu investieren.
Vorab bemerkt: beides hat sich gelohnt.

Bild 1.
Der Silmaril im neuen Glanz. Ich habe ihn komplett zerlegt und den braunen Metallbelag mit Scheuermilch entfernt (die Wasserreste lassen sich gut mit Spiritus ausspülen, dann landet später nicht so viel Wasserdampf in der Vakuumpumpe). Dank des modularen Aufbaues ließen sich die Schliffe mit den Schlaucholiven einfach gegen Übergangsstücke mit DN16- Flanschen austauschen. Links sieht man die Pirani- Meßröhre, die die Hilfskathode ersetzt.

Bild 2.
Das modifizierte Vakuumsystem. Der dicke Metallbalgen- Schlauch ist links silbern zu erkennenen. Direkt an der Pumpe sitzt der DN16- Vakuumhahn. Links unten das Anzeigeinstrument des Pirani- Vakuummeters zu sehen. Es zeigt bei diesem Test 20 Pa (1.5 * 10^-1 Torr) an. Die Helium- Zuleitung ist noch in der ursprünglichen Form, allerdings habe ich das Quecksilber- Barometer entfernt.

Ein gewisses Problem stellt der Betrieb des Pirani- Vakuummeters mit Helium dar. Das Gerät ist zunächst einmal natürlich für Luft geeicht und zeigt bei Betrieb mit Helium falsche Werte an. Wie man aus Tabellen in der Fachliteratur entnehmen kann, ist der Unterschied im niedrigen Druckbereich aber eine Konstante. Wegen der besseren Wärmeleitung von Helium zeigt das Instrument also einen zu hohen Druck an.
Natürlich habe ich das gegen meine anderen Meßgeräte getestet, mit folgendem Ergebnis: die Meßröhre ist für Helium oberhalb 930 Pa (7 Torr) unbrauchbar (es wird Atmosphärendruck angezeigt). Zwischen 133 und 800 Pa wird in erster Näherung doppelt soviel Heliumdruck wie vorhanden angezeigt, unter 133 Pa (1 Torr) konstant 1.5 mal soviel. In diesem interessanten Bereich muß also einfach die Anzeige durch 1.5 geteilt werden.
Mit dem neuen Metallschlauch kann die Pumpe nun richtig ihre Muskeln spielen lassen. Es ist problemlos möglich, im Helium- Durchfluß bis 13 Pa (0.1 Torr) herunterzugehen, das Spektroskop zeigt dabei, daß das Helium noch relativ rein ist. Bei noch niedrigerem Druck scheint eher die Rückdiffusion von Pumpenöl als Luftreste das Problem zu sein. Die Pumpe ist hier an der Grenze ihrer Leistungsfähigkeit angelangt.

Bild 3.
Bei 13 Pa (0.1 Torr, 100 Micron) Helium formiert der Fokus im inneren Gitter sich schon sehr viel deutlicher. Die Farben entsprechen jetzt denen in der klassischen Helium- Entladung: Plasma rosa, Elektronenstrahl grün. Der Fokus selbst zieht sich diffus in das Zentrum zusammen und wird dort etwas heller.
Auf dem Bild leider nicht zu erkennen sind eine Art schwacher, nach außen geworfener Schatten im rosa Glimmen außerhalb des Gitters. Sie sind vielleicht ein Hinweis auf einsetzende Rezirkulation der Helium- Ionen.

Bild 4.
Gleiche Bedingungen wie oben, längere Belichtung und größerer Bildausschnitt. Gegenüber dem Betrieb bei höherem Druck zieht der Kelch des Elektronenstrahles sich bei 13 Pa wesentlich stärker zusammen. An der Stelle, an der die Glaswand getroffen wird, ist bläuliche Fluoreszenz zu sehen. Das Glas wird dort so heiß, daß es kaum noch angefaßt werden kann.
Die Gitterspannung stieg bei den Bedingungen dieser Versuche schon auf 1000 Volt an.

Hinunter zum Hochvakuum

Nach langer Zeit habe ich endlich mal Zeit, wieder ein Update zu schreiben. Schon 2009 habe ich nämlich eine kleine Diffusionspumpe angeschafft, die in ihrer Größe zur Leistung meiner Vorpumpe paßt. Generell gilt: die Vorpumpe sollte ein Endvakuum von 13 Pa erreichen können (0.1 Torr), und sie sollte so 2 m³ pro Stunde wegschaufeln können. Meine einstufige Drehschieberpumpe (inzwischen schon 20 Jahre alt, aber immer moch top) kann das.
Im Dezember 2010 habe ich dann auch endlich die lang geplante Kaskade zusammengestellt. Auslöser war allerdings eine CO₂-Laserröhre, die damit auch gut betrieben werden kann (siehe meine Laserseite).

Bild 1.
Der Silmaril im wiederum gewachsenen Kreis der zugehörigen Labormodule. Ganz hinten links in der Ecke die blaue Drehschieberpumpe, davor silbern und aufrecht stehend die Öldiffusionspumpe, beides mit Metallbalgenschläuchen verbunden. Vorne links die Flasche mit Ballonhelium und das Pirani-Vakuummeter.
Hinter dem gläsernen Silmaril ein Variac, der zwei Neontrafos kontrolliert, die ihrerseits die Doppelkaskade versorgen. Letztere ist zur Zeit noch nicht voll ausgebaut, die Maximalspannung liegt bei 22.4kV.
Das Bild wurde während des Abpumpens mit der Diffusionspumpe aufgenommen.

Bild 2.
Mein schrottiger Fotoapparat hat mich hier im Stich gelassen, die Farben stimmen überhaupt nicht, und die Strahlen des Sternmodus sind fast nicht zu erkennen.
Der Silmaril läuft hier bei einem Druck von 2.7 Pa Helium (etwa 20 Micron) bei 5mA Entladungsstrom. Die Gitterspannung steigt auf immerhin 12kV an. Visuell zu sehen ist ein vielstrahliger rosafarbener Stern, dessen Strahlen nadeldünn fast bis zur Anode reichen. Der Plasmafokus ist sehr klein (~1mm). Die Glaswände der gesamten Hauptkammer fluoreszieren sehr stark blaugün.
Bedingt durch die enge Kathodenspirale sieht der Stern im Silmaril ganz anders aus als bei den üblichen Amateurfusoren mit wenigen Drahtringen und großen Öffnungen, die meistens 6 dickere Sternstrahlen ausbilden. Die vielen dünnen Strahlen im Silmaril vermitteln ein atemberaubendes räumliches Empfinden, da sie durch das Glasgefäß aus vielen Blickwinkeln betrachtet werden können.

Bei dem niedrigen Druck und der hohen Spannung ist der Betrieb allerdings schon eine echte Geschicklichkeitsübung. Das Gas wird langsam zu dünn, um noch eine Entladung aufrechterhalten zu können, und bedarf dafür der aus der beinahe glühenden Kathode emittierten Elektronen. Es ist mit Geschick möglich, den Druck zu senken, dabei den Entladungsstrom gegenzuregeln (durch Erhöhen der Spannung), damit die Kathode schön heiß bleibt, und auf diese Weise zu immer tieferen Drücken zu gelangen. Geht die Entladung aus, dann kühlt die Kathode ab, und man kann auch mit der maximalen Spannungseinstellung nicht wieder zünden. Auf diese Weise bin ich bisher bis 2.4 Pa / 12.5kV gekommen. Die Kathode glüht dann schon dunkelrot.
Möglicherweise könnte eine aktiv geheizte Kathode hier helfen.

Links

Fusor.net - was auch immer der interessierte Laie über einen Fusor wissen will, hier ist der beste Startpunkt für die Suche.

Wikipedia - Der Eintrag über den Fusor und Philo Farnsworth bei Wikipedia.

NIST - Datenbank mit Angaben zur Spektroskopie von Helium und anderen Gasen.

Fusor Math - Jim Lux' Website über einfache Berechnungen zum Thema Fusor.

*

Danksagung
Mein Dank gilt Christine Seibel für die Photos von der Glimmröhre und der Kathodenstrahlröhre und Christiane Buck für die ersten Photos vom Silmaril.

*

Referenzen

[1] Wien / Harms:
    Handbuch der Experimentalphysik 
    Bd. XIII,3: Selbstständige Entladung in Gasen
    Akademische Verlagsgesellschaft Leipzig (1929)
    
[2] Wien / Harms:
    Handbuch der Experimentalphysik 
    Bd. XIV: Kathoden- und Kanalstrahlen
    Akademische Verlagsgesellschaft Leipzig (1929)
    
[3] Gmelins Handbuch der Anorganischen Chemie
    System-Nr.1: Edelgase
    Verlag Chemie, Weinheim (1926)
    
[4] Nomoto, K., Thielemann, F.-K., Miyaji, S.:   
    The triple alpha reaction in accreting white dwarfs  
    and neutron stars,                             
    Astron. Astrophys. 149(1985) p.239        
   
[5] Adelberger, E. G. et al:     
    Solar fusion cross sections      
    Rev. Mod. Phys. 70(1998) p.1265  
    
[6] Papadopoulos & Serafetinides:
    Investigation of the electrical characteristics of charge transfer circuits 
    used in gas laser excitation,
    J. Appl. Phys. D 24(1991) p.1917 
     
[7] Flügge, E. (Hrsg):
    Handbuch der Physik (Encyclopedia of Physics), 
    Bd. XLIV: Nuclear Instrumentation I,
    Springer Verlag, Berlin (1959)

Back to Diane's HomePage